The Fisher Effect demonstrates the connection between real interest rates, nominal interest rates, and the rate of inflation. According to the Fisher Effect, the real interest rate is equal to the nominal interest rate minus the expected rate of inflation (note that in this equation, all rates used should be compounded).
The result, in practice, is that as inflation rates go up, real interest rates go down, when nominal rates don’t increase at rates equal to those of inflation. This effect is not always immediately visible, but over time, it is a consistent economic pattern.
The Fisher Effect Equation
Here is the fisher effect equation described above again, in the most simplified terms:
r = i – π
In this equation, i is the nominal interest rate; r is the real interest rate; and π is the rate of inflation. A more exact and complicated formula for the Fisher equation is as follows:
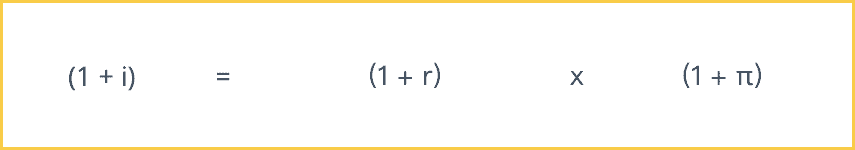
(1 + i) = (1 + r) (1 + π)
The Fisher Effect Equation Example
If, for instance, inflation is 4% annually and the nominal interest rate is 10%, every dollar in the bank becomes $1.10 next year. But because inflation is 4%, that $1.10 can only purchase 6% more goods and services (rather than 10%), which makes the real interest rate 6%. Here it is plugged into the equation above:
6% [r] = 10% [i] – 4% [π]
r = 6% (real interest rate)
i = 10% (nominal interest rate)
π = 4% (rate of inflation)
The Link between Inflation and Nominal Interest Rates
Nominal interest rates tend to run parallel to inflation rates so that monetary policy is effectively neutralized. More specifically, when the money supply is increased by a central bank, and expected inflation rises, that central bank also increases interest rates. And when nominal interest rates increase simultaneously with inflation rates, that means that there is little practical effect.
Limitations of the Fisher Effect
One significant limitation of this concept is when liquidity traps occur (when savings rates are high and interest rates are low, and consumers refrain from the use of bonds), lowering nominal interest rates may not sufficiently help to increase spending and investment.
Another issue is the elasticity of demand with regard to interest rates–when assets are increasing in price and when consumer confidence is high, having high real interest rates will not necessarily decrease demand, so central banks would have to increase the real interest rate further in order to do so.
Finally, sometimes the interest rates that banks use differs from the base rate decided upon by central banks.
Importance with Regard to Money Supply
The Fisher Effect demonstrates the way that the money supply influences inflation rate and nominal interest rate together. For instance, when monetary policy shifts in a way that increases the inflation rate by 5 percent, the result is that the nominal interest rate also increases by that same percentage.
While alterations in the money supply do not alter the real interest rate, changes in the nominal interest rate are associated with alterations in the money supply.

